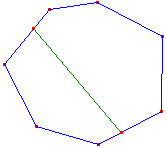
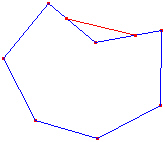
Voici un exemple de polygone convexe et un non convexe :
Voici l'exemple de l'ennéagone régulier :
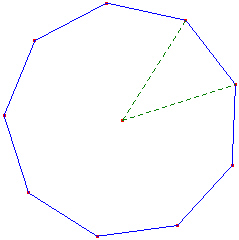
Les polygones réguliers
Considérons un polygone à n côtés.
On dit qu'un tel polygone est régulier lorsque :



Un polygone régulier est donc inscriptible dans un cercle dont le centre est celui de la rotation.
Si l'on note R le rayon du cercle circonscrit à un polygone régulier à n côtés, on peut déterminer en fonction de R et n :
En se plaçant dans un triangle formé par le centre du polygone, un sommet et un sommet consécutif, par exemple A0OA1:
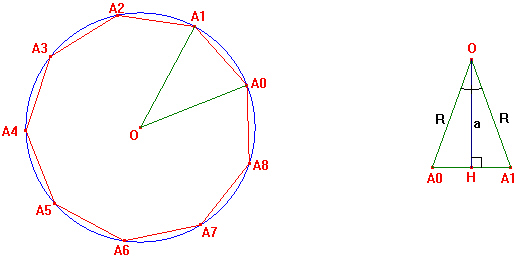
Dans le triangle rectangle A0OH, l'angle en O est de 180°/n, donc a = R×cos(180°/n) ; HA0 = R×sin(180°/n) d'où A0A1 = 2R×sin(180°/n) et donc p = 2nR×sin(180°/n).
L'aire du triangle A0OA1 est A0A1×OH/2 = R²×cos(180°/n)×sin(180°/n) = R²×sin(360°/n)/2.
D'où l'aire du polygone est A = nR²×sin(360°/n)/2.
Voici un récapitulatif de ces valeurs en prenant R=1.
Les cellules sans valeurs signifient qu'une valeur exacte exprimable par radicaux n'existe pas.
d (valeur exacte) |
d (valeur approchée) |
p (valeur exacte) |
p (valeur approchée) |
A (valeur exacte) |
A (valeur approchée) |
a (valeur exacte) |
a (valeur approchée) |
|
| n=3 | √3 |
1,73 |
3√3 |
5,2 |
3√3/4 |
1,3 |
1/2 |
0,5 |
| n=4 | √2 |
1,41 |
4√2 |
5,66 |
2 |
2 |
√2/2 |
0,71 |
| n=5 | √(10-2√5)/2 |
1,18 |
5√(10-2√5)/2 |
5,88 |
5√(10+2√5)/8 |
2,38 |
(1+√5)/4 |
0,81 |
| n=6 | 1 |
1 |
6 |
6 |
3√3/2 |
2,6 |
√3/2 |
0,87 |
| n=7 | 0,87 |
6,1 |
2,74 |
0,9 |
||||
| n=8 | √(2-√2) |
0,77 |
8√(2-√2) |
6,12 |
2√2 |
2,83 |
√(2+√2)/2 |
0,92 |
| n=9 | 0,68 |
6,16 |
2,9 |
0,94 |
||||
| n=10 | (√5-1)/2 |
0,62 |
5(√5-1) |
6,18 |
5√(10-2√5)/4 |
2,94 |
√(10+2√5)/4 |
0,95 |
| n=11 | 0,56 |
6,2 |
2,97 |
0,96 |
||||
| n=12 | (√6-√2)/2 |
0,52 |
6(√6-√2) |
6,21 |
3 |
3 |
(√6+√2)/4 |
0,97 |
| n=13 | 0,48 |
6,22 |
3,02 |
0,97 |
||||
| n=14 | 0,45 |
6,23 |
3,04 |
0,97 |
||||
| n=15 | (√(5+√5)-√(9-3√5))/(2√2) |
0,42 |
15(√(5+√5)-√(9-3√5))/(2√2) |
6,24 |
15(√15+√3-√(10-2√5))/16 |
3,05 |
(√5-1+√(6√5+30))/8 |
0,98 |
| n=16 | √(2-√(2+√2)) |
0,39 |
16√(2-√(2+√2)) |
6,24 |
4√(2-√2) |
3,06 |
√(2+√(2+√2))/2 |
0,98 |
| n=17 | √(17-√17-√(34-2√17)-√(68+12√17+2√(34-2√17)×(√17-1)-16√(34+2√17)))/√8 |
0,37 |
17√(17-√17-√(34-2√17)-√(68+12√17+2√(34-2√17)×(√17-1)-16√(34+2√17)))/√8 |
6,25 |
17√((17-√17-√(34-2√17)-√(68+12√17-2√(34-2√17)+2√(34(17-√17))-16√(34+2√17)))(15+√17+√(34-2√17)+√(68+12√17-2√(34-2√17)+2√(34(17-√17))-16√(34+2√17))))/32 |
3,07 |
√(15+√17+√(34-2√17)+√(68+12√17+2√(34-2√17)×(√17-1)-16√(34+2√17)))/(4√2) |
0,98 |
| n=18 | 0,35 |
6,25 |
3,08 |
0,98 |
||||
| n=19 | 0,33 |
6,25 |
3,08 |
0,99 |
||||
| n=20 | (√10+√2-2√(5-√5))/4 |
0,31 |
5(√10+√2-2√(5-√5)) |
6,26 |
5(√5-1)/2 |
3,09 |
√(8+2√(10+2√5))/4 |
0,99 |
Si vous voulez une version téléchargeable, cliquez sur LATEX.
I) Construction de polygones réguliers selon le nombre de côté n.
Pour n=3.
Dans ce cas le tétragone régulier est un triangle équilatéral.
- Soit O un point quelconque du plan.
- Considérons un cercle de centre O et de rayon quelconque.
- Soit A0 un point quelconque de ce cercle, considérons le point A0' le point diamétralement opposé à A0.
- Soit (d) la médiatrice
de [OA0], cette droite coupe le cercle en deux points : A1 et A2.
-
Le triangle A0A1A2 est équilatéral.
Pour n=4.
Dans ce cas le tétragone régulier est un carré.
- Soit O un point quelconque du plan.
- Considérons un cercle de centre O et de rayon quelconque.
- Soit A0 un point quelconque de ce cercle, considérons le point A2 le point diamétralement opposé à A0.
- Soit (d) la médiatrice de [A0A2], cette droite coupe le cercle en deux points : A1 et A3.
- Le quadrilatère A0A1A2A3 est un carré.
Pour n=5.
Ce polygone régulier est un pentagone régulier.
- Soit O un point quelconque du plan.
- Considérons un cercle de centre O et de rayon quelconque.
- Soit A0 un point quelconque de ce cercle, considérons le point A0' le point diamétralement opposé à A0.
- Soit I1 le milieu su segment [OA0'].
- Soit (d) la médiatrice du segment [A0A0'], cette droite coupe le cercle en deux points J1 et J2.
- L'arc de cercle de centre I1 joignant J1 et J2 coupe le segment [OA0] en un point I2.
- La médiatrice du segment [OI2] coupe le cercle en deux points A1 et A4.
- En reportant la mesure A0A1 à partir du point A1 sur le cercle on obtient les points A2 et A3.
Dans le cas n=5, on peut relier les points du pentagone régulier de façon différente de sorte à former un polygone étoilé stable par rotation d'angle 72°.
On nomme usuellement ce polygone étoilé par pentagramme.
Pour construire ce pentagramme, il suffit de relier les points du pentagone régulier de 2 en 2.
Pourquoi de 2 en 2 car PGCD(2;n)=1.
Par un calcul simple, les seuls entiers étant premiers avec n sont : 1 ; 2 ; 3 et 4.
Relier de 1 en 1 ou de 4 en 4 nous donne le même polygone (on relie juste dans l'autre sens) : le pentagone régulier, de même il est équivalent de relier de 2 en 2 ou de 3 en 3 pour obtenir le pentagramme.
Ainsi, il n'existe que le pentagone régulier et le pentagramme.
Pour n=6.
Ce polygone est un hexagone régulier.
Pour construire ce polygone, il suffit de partir du triangle équilatéral et de construire son symétrique par rapport à O, ou de construire les médiatrices des côtés adjacents.
Pour n=7.
Ce polygone est un heptagone régulier qui n'est pas constructible à la règle et au compas.
Le rapporteur est donc nécessaire pour construire ce polygone.
Comme dans le cas du pentagone régulier, on peut ici aussi construire des heptagrammes en reliant de 2 en 2 ou de 3 en 3.
Pour n=8.
Ce polygone est un octogone régulier, on peut le construire en traçant les médiatrices des côtés adjacents du carré.
On peut construire ici aussi un octogramme en reliant les points de l'octogone de 3 en 3.
Pour n=9.
Ce polygone régulier est un ennéagone régulier qui n'est pas constructible à la règle et au compas. Ici aussi on a besoin du rapporteur.
On peut construire un décagramme en reliant de 3 en 3 les sommets du décagone régulier.
Pour n=11.
Ce polygone régulier est un hendécagone que l'on peut pas construire à la règle et au compas. Il nous faut donc un rapporteur.
On peut construire quatre hendécagrammes en reliant de 2 en 2, de 3 en 3, de 4 en 4 et de 5 en 5.
Si n=12.
Ce polygone régulier est un dodécagone.
Pour le construire on procède comme suit :
- Construire comme on l'a vu un carré A0A3A6A9 et un triangle équilatéral A0A4A8 inscrits dans un cercle ayant pour point commun le point initial A0.
- Reporter la longueur A3A4 le long du cercle pour obtenir les autres points.
Il existe un dodécagramme en reliant de 5 en 5 :
Si n=13.
Ce polygone régulier est un triskaidécagone non constructible à la règle et au compas, voici donc une construction au rapporteur :